티스토리 뷰
문제 출처 : algospot.com :: POLY
algospot.com :: POLY
폴리오미노 문제 정보 문제 정사각형들의 변들을 서로 완전하게 붙여 만든 도형들을 폴리오미노(Polyomino)라고 부릅니다. n개의 정사각형으로 구성된 폴리오미노들을 만들려고하는데, 이 중 세로
algospot.com
1. 완전 탐색에서 시작하기
- 먼저 세로 단조 폴리오미노에서 각 가로줄(행)에 포함된 정사각형들은 항상 일렬로 연속되어 있다.
- 따라서 각각의 가로줄마다 몇 개의 정사각형이 연속되어 있는지 결정하고 이를 좌-우로 적절하게 움직이면(세로 단조 폴리오미노의 조건을 만족하도록) 모든 폴리오미노를 만들 수 있다.
- 폴리오미노가 전체적으로 n개의 정사각형으로 이루어져 있다고 할 때
- 첫 번째 가로줄의 사각형을 1개부터 n개까지 분류하여 각각의 경우에 따라 나오는 폴리오미노의 수를 모두 더하면 원하는 답을 찾을 수 있다.
- 첫 줄에 i개의 정사각형이 속한 폴리오미노는 나머지 n-i개로 구성된 폴리오미노를 만들고 이를 첫 줄에 붙여주면 된다.
- 이런 방식으로 첫 번째 줄에 대해 first개의 정사각형을 배치하고
- 나머지 n-first개의 정사각에 대해 다시 재귀적인 호출을 통해 전체 세로 단조 폴리오미노의 수를 계산할 수 있다.
2. 부분 문제 정의
- poly(n, first) = n개의 정사각형을 포함하되, 첫 줄에는 first개의 정사각형이 들어가는 폴리오미노의 수
- 첫 줄에 first개의 정사각형이 정해졌으니 연결방법을 고려하지 않은 두번째 줄 부터 이제 남은 n-first개의 정사각형으로 폴리오미노를 만드는 방법의 수는 다음과 같다.
- poly(n-first, 1) + poly(n-first, 2) + poly(n-first, 3) + ... + poly(n-first, n-first)
- 위 과정은 n개의 정사각형을 이용해 폴리오미노의 각 줄에 몇 개의 정사각형을 배치하는지를 의미한다.
- 이제 각 줄에 있는 정사각형이 어떻게 연결되는지를 고려한 경우의 수를 계산해야 한다.
- 폴리오미노에서 첫번째 줄과 두번째 줄에 정사각형의 수에 따라 두 줄을 연결하는 경우의 수가 다르다.
- 예를 들어, 첫줄에 2개의 정사각형과 두번째 줄에 3개의 정사각형이 있는 폴리오미노의 모습은 아래의 그림과 같이 총 (2 + 3 - 1 = 4) 가지가 존재한다.

- 이를 일반화 하면 첫 번째 줄에 first, 두번째 줄에 second개의 정사각형이 있는 폴리오미노의 연결 방식은 (first + second - 1)로 표현할 수 있다.
- 결과적으로 n개의 정사각형 중 첫 줄에 first개가 정해진 폴리오미노를 만드는 방법의 수는 아래와 같다.
- (first + 1 - 1) * poly(n-first, 1) + (first + 2 - 1) * poly(n-first, 2) + ... + (first + n - first - 1) * poly(n-first, n-first)
- 이때 n과 first는 각각 0부터 100까지 범위 내의 정수이므로 쉽게 메모이제이션을 적용해 동적 계획법으로 바꿀 수 있다.
- 점화식은 아래와 같다.
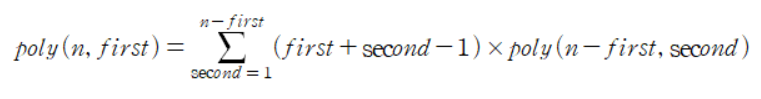
3. 코드 - 풀이 해설 방법
MOD = int(10e7)
# n개의 정사각형에 대해서 첫 줄이 first개인 폴리오미노의 수를 반환
def poly(n, first):
# 기저 사례 : 한 줄을 모든 사각형으로 구섣
if n == first:
return 1
# 메모이제이션
if cache[n][first] != -1:
return cache[n][first]
cache[n][first] = 0
# second는 최대 n-first까지 증가할 수 있음을 유의!
# range(1, n-first)는 틀림...
for second in range(1, n-first+1):
add = first + second - 1 # 첫 번째 줄과 연결될 수 있는 하위 폴리오미노의 경우의 수
add *= poly(n-first, second) # 경우의 수 * 만들 수 있는 폴리오미노 모양의 수
add %= MOD
cache[n][first] += add
cache[n][first] %= MOD
return cache[n][first]
for tc in range(int(input())):
n = int(input())
cache = [[-1] * (n+1) for _ in range(n+1)]
answer = 0
# 첫 번째 줄의 사각형이 1개 있는 경우부터 해서 n개 있는 경우까지 합
for first in range(1, n+1):
answer += poly(n, first)
print(answer % MOD)- 코드 하단의 문제 입-출력 부분에서 first의 값을 1부터 n까지의 모든 경우를 다 고려해서 합한 결과를 반환해야 하는 것을 유의해야 한다.
- 문제에서 가능한 n과 first의 조합의 수는 O(n^2)이고, poly() 함수를 한 번 계산하는데 O(n)의 시간이 들기 때문에 전체 시간 복잡도는 O(n^3)이 된다.
4. 후기
개인적으로 문제 풀이 방법을 공부하면서 재미있었다. 이전 8.9 단원에서 공부했던 Quantization 문제와 같이 수식으로 풀어도 그 개념이 직관적으로 이해되는 것처럼 문제의 점화식을 유도하는 과정이 복잡하지 않고 간단한 개념만으로도 해결할 수 있을때 재미를 느낄 수 있었던 것 같다. 근데 이후에는 확률에 대한 부분들이 나오는데 이 부분들은 수식을 봐도 쉽게 이해가 되지 않아 굉장히 난처하다.
처음에 코딩 테스트를 공부하기 전에는 복잡하게 설명된 문제를 간략화해서 코딩으로 구현하는 공부를 하지 않을까 예상했었는데 막상 종만북하고 다른 책을 공부하면서 느낀 점은 코딩은 부가적인 것이고 어떻게 문제를 해석하고 설계해야 하는지가 더 중요한 부분으로 다가온다. 간단하게 이야기하면 개인적으로는 코딩 테크닉을 향상하기 위한 공부를 기대하고 시작했지만 흔히 말하는 컴퓨팅적 사고력을 중점적으로 공부하게 되는것 같다.
여러 라이브러리나 API 혹은 패키지들을 효율적으로 사용하는 것이 중요한지 혹은 이런 컴퓨팅적 사고력이 중요한지는 모르겠지만 뭐든 하나 알고있다면 도움이 되리라 기대해본다.
LeeSeok-Jun/Algorithmic_Problem_Soving_Strategies
프로그래밍 대회에서 배우는 알고리즘 문제해결 전략. Contribute to LeeSeok-Jun/Algorithmic_Problem_Soving_Strategies development by creating an account on GitHub.
github.com
'프로그래밍 대회에서 배우는 알고리즘 문제해결 전략 > 8장_동적 계획법' 카테고리의 다른 글
| 8.16 문제 : 두니발 박사의 탈옥(Python) - 마르코프 연쇄 (0) | 2021.04.13 |
|---|---|
| 8.12 문제 : 비대칭 타일링(Python) (0) | 2021.04.09 |
| 8.11 경우의 수와 확률(2)_우물을 기어오르는 달팽이(Python) (0) | 2021.04.09 |
| 8.11 경우의 수와 확률(1)_타일링 방법의 수 세기, 삼각형 위의 최대 경로 개수 세기(Python) (0) | 2021.04.08 |
| 8.9 문제 : Quantization(Python) (0) | 2021.03.31 |
- Total
- Today
- Yesterday
- k번째 답 계산하기
- 비트 마스크
- 마르코프 연쇄
- 프로그래밍 대회에서 배우는 알고리즘 문제해결전략
- 동적 계획법
- 프로그래머스
- 탐욕법
- 카카오
- 난이도:하
- 프로그래밍 대회에서 배우는 알고리즘 문제 해결 전략
- 프로그래밍 대회에서 배우는 알고리즘 문제해결 전략
- 파이썬
- 난이도:상
- 그리디
- 난이도:중
- 종만북
- python
- 구현
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
